Science
By Sadaputa Dasa
“Probability is the most important concept in modern science,
especially as nobody has the slightest idea what it means.
—Bertrand Russell

Throughout human history, philosophers and seekers of knowledge have sought to discover a single fundamental cause underlying all the phenomena of the universe, Since the rise of Western science in the late Renaissance, many scientists have also felt impelled to seek this ultimate goal, and they have approached it from their own characteristic perspective. Western science is based on the assumption that the universe can be understood mechanistically—that is, in terms of numbers and mathematical formulas—and Western scientists have therefore searched for an ultimate, unified mathematical description of nature.
This search has gone through many vicissitudes, and many times scientists have felt that a final, unified theory was nearly within their grasp. Thus in the middle of the nineteenth century the physicist Hermann von Helmholtz was convinced that “The task of physical science is to reduce all phenomena of nature to forces of attraction and repulsion, the intensity of which is dependent only upon the mutual distance of material bodies.” ** (Hermann von Helmholtz, “Uber die Erhaltung der Kraft,” Osrwald’s Klassiker der Exakten Wissenschaft, Nr. 1, 1847, p.6.) By 1900 many new concepts and discoveries had been incorporated into the science of physics. and Helmholtz’s program had become superannuated. At about this time, however, Albert Einstein embarked on a much more sophisticated and ambitious program of unification. His goal was to explain all the phenomena of the universe as oscillations in one fundamental “unified field.” But even while Einstein was working on this project, revolutionary developments in the science of physics were rendering his basic approach obsolete. For several decades a bewildering welter of new discoveries made the prospect of finding an ultimate theory seem more and more remote. But the effort to find a unified theory of nature has continued, and in 1979 three physicists (Sheldon Glashow, Abdus Salem, and Steven Weinberg) won the Nobel Prize in physics for their effort in partially tying together some of the disparate elements of current physical theories. On the basis of their work, many scientists are now optimistically anticipating the development of a theory that can explain the entire universe in terms of mathematical equations describing a single, primordial “unified force.”
The scientists’ search for a unified explanation of natural phenomena begins with two main hypotheses. The first of these is that all the diverse phenomena of nature derive in a harmonious way from some ultimate, unified source. The second is that nature can be fully explained in terms of numbers and mathematical laws. As we have pointed out, the second of these hypotheses constitutes the fundamental methodological assumption of modern science, whereas the first has a much broader philosophical character.
Superficially, these two hypotheses seem to fit together nicely. A simple system of equations appears much more harmonious and unified than a highly complicated system containing many arbitrary, unrelated expressions. So the hypothesis that nature is fundamentally harmonious seems to guarantee that the ultimate mathematical laws of nature must be simple and comprehensible. Consequently, the conviction that nature posesses an underlying unity has assured many scientists that their program of mechanistic explanation is feasible.
We will show in this article, however, that these two hypotheses about nature are actually not compatible. To understand why this is so, we must consider a third feature of modern scientific theories—the concept of chance.
As we carefully examine the role chance plays in mechanistic explanations of nature, we shall see that a mechanistic theory of the universe must be either drastically incomplete or extremely incoherent and disunited. It follows that we must give up either the goal of mechanistically explaining the universe, or the idea that there is an essential unity behind the phenomena of nature. At the end of this article we will explore the first of these alternatives by introducing a nonmechanistic view of universal reality, a view that effectively shows how all the diverse phenomena of nature derive from a coherent, unified source.
First, however, let us examine how scientists employ the concept of chance in mechanistic theories of the universe. Such theories are normally formulated in the mathematical language of physics, and they involve many complicated technical details. Yet the basic concepts of chance and natural law in current physical theories readily lend themselves to illustration by simple examples. We will therefore briefly contemplate a few such examples and then draw some general conclusions about universal mechanistic theories.
Figure 1 depicts a simple device we shall regard, for the sake of argument, as a model universe. This device consists of a box with a window that always displays either a figure 0 or a figure 1. The nature of this box is that during each consecutive second the figure in the window may either remain unchanged or else change exactly once at the beginning of that second. We can thus describe the history of this model universe by a string of zeros and ones representing the successive figures appearing in the window during successive seconds. Figure 2 depicts a sample history.
Let us begin by considering how the concept of chance could apply to our model universe. For example, suppose we are told that the model universe obeys the following statistical law:
The zeros and ones appear randomly in the window, independently of one another. During any given second the probability is 50% that the window will display a one and 50% that it will display a zero.
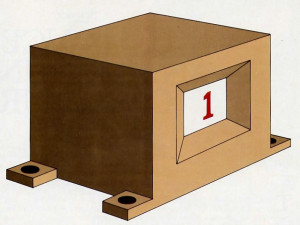
How are we to interpret this statement? As we shall see, its interpretation involves two basic questions: the practical question of how we can judge whether or not the statement is true, and the broader question of what the statement implies about the nature of our model universe.
The answer to the first question is fairly simple. We would say that the statement is true of a particular history of ones and zeros if that history satisfied certain statistical criteria. For example, if the probability for the appearance of one is to be 50%, we would expect roughly 50% of the figures in the historical sequence to be ones. This is true of the sample history in figure 2, where the percentage of ones is 49.4%.
We could not, however, require the percentage of ones to be exactly 50%. If the sequence itself is random, the percentage of ones in the sequence must also be random, and so we would not expect it to take on some exact value. But if the percentage of ones were substantially different from 50%, we could not agree that these ones were appearing in the window with a probability of 50%.
In practice it would never be possible for a statistical analyst to say definitely that a given history does or does not satisfy our statistical law. All he could do would be to determine a degree of confidence in the truth or falsity of the law as it applied to a particular sequence of ones and zeros. For example, our sample history is 979 digits long. For a sequence of this length to satisfy our law, we would expect the percentage of ones to fall between 46.8% and 53.2%. (These are the “95% confidence limits.”) If the percentage did not fall within these limits, we could take this failure as an indication that the sequence did not satisfy the law, but we could not assert this as a definite conclusion.
We have seen that our sample history consists of approximately 50% ones. This observation agrees with the hypothesis that the sequence satisfies our statistical law, but it is not sufficient to establish this, for there are other criteria such a sequence must meet. For example, suppose we divide the sequence into two-digit subsequences. There are four possible subsequences of this type, namely 00, 01, 10, and 11. If the ones and zeros were indeed appearing at random with equal probability, we would expect each of these four subsequences to appear with a frequency of roughly 25%. In fact, these subsequences do appear in our sample history with frequencies of 25.6%, 24.7%, 25.4%, and 24.3% respectively, and these frequencies also agree with the hypothesis that this history satisfies the statistical law.
In general, we can calculate the frequencies of subsequences of many different lengths. A statistical analyst would say that the history obeys our statistical law if subsequences of equal length always tend to appear with nearly equal frequency. (By “nearly equal” we mean that the frequencies should fall within certain calculated confidence limits.)
Introducing “Absolute Chance”
So in practical terms we can interpret our statistical law as an approximate statement about the relative frequency of various patterns of ones and zeros within a larger sequence of ones and zeros. If statistical laws were never attributed a deeper meaning than this, the concepts of randomness and statistical law might seem of little interest. However, because of an additional interpretation commonly given them, these concepts are actually of great significance in modern science, and particularly the science of physics. This interpretation becomes clear in the following reformulation of our statistical law, as understood from the viewpoint of modern physics:
The box contains some apparatus that operates according to definite laws of cause and effect and that determines which figures will appear in the window. But in addition to its predictable, causal behavior, this apparatus periodically undergoes changes that have no cause and that cannot be predicted, even in principle. The presence of a one or a zero in the window during any given second is due to an inherently unpredictable, causeless event. Yet it is also true that ones and zeros are equally likely to appear, and thus we say that their probability of appearance is 50%.
In this formulation, our statistical law is no longer simply a statement about patterns of ones and zeros in a sequence. Rather, it now becomes an assertion about an active process occurring in nature-a process that involves absolutely causeless events. Such an unpredictable process is said to be a “random process” or a process of “absolute chance.”
When modern physicists view our statistical law in this way, they still judge its truth or falsity by the same criteria involving the relative frequencies of patterns of ones and zeros. But now they interpret the distribution of these patterns as evidence for inherently causeless natural phenomena. Ironically, they interpret the lawlike regularities the frequencies of various patterns obey as proof of underlying causeless events that, by definition, obey no law whatsoever.
At first glance this interpretation of the concept of randomness may seem quite strange, even self-contradictory. Nonetheless, since the development of quantum mechanics in the early decades of the twentieth century, this interpretation has occupied a central place in the modern scientific picture of nature. According to quantum mechanics, almost all natural phenomena involve “quantum jumps” that occur by absolute, or causeless, chance. At present many scientists regard the quantum theory as the fundamental basis for all explanations of natural phenomena. Consequently, the concept of absolute chance is now an integral part of the scientific world view.
The role absolute chance plays in the quantum theory becomes clear through the classical example of radioactive decay. Let us suppose our model universe contains some radioactive atoms, a Geiger counter tube, and some appropriate electrical apparatus. As the atoms decay they trigger the Geiger counter and thereby influence the apparatus, which in turn controls the sequence of figures appearing in the window. We could arrange the apparatus so that during any given second a one would appear in the window if a radioactive decay occurred at the start of that second, and otherwise a zero would appear. By adjusting the amount of radioactive substance, we could control the average rate at which the counter was triggered and thus assure that the figure one would appear approximately 50% of the time.

If the apparatus were adjusted in this way, we would expect from observational experience that the sequence of ones and zeros generated by the model universe would satisfy our simple statistical law. Modern physicists interpret this predictable statistical behavior as evidence of an underlying process of causeless chance. Although they analyze the operation of the apparatus in terms of cause and effect, they regard the decay of the atoms themselves as fundamentally causeless, and the exact time at which any given atom decays as inherently unpredictable. This unpredictability implies that the sequence of ones and zeroes generated by the model should follow no predictable pattern. Thus the hypothesis of causeless chance provides an explanation of the model’s statistical behavior.
If we analyze the above example of a physical system, we can see that it involves a mixture of two basic elements: determinism and absolute chance. In our example we assumed that the electrical apparatus followed deterministic laws, whereas we attributed the decay of the radioactive atoms to absolute chance. In general, the theories of modern physics entail a combination of these two elements. The deterministic part of the theory is represented by mathematical equations describing causal interactions, and the element of chance is represented by statistical laws expressed in terms of probabilities.
When some scientists view natural phenomena in the actual universe as obeying such combined deterministic and statistical laws, they show a strong tendency to suppose that the phenomena are governed by these laws, and by nothing else. They are tempted to imagine that the laws correspond directly to a real underlying agency that produces the phenomena. Once they visualize such an agency, they naturally think of it as the enduring substantial cause, and they regard the phenomena themselves as ephemeral, insubstantial effects.
Thus the physicist Steven Weinberg refers to the theories of physics as “mathematical models of the universe to which at least the physicists give a higher degree of reality than they accord the ordinary world of sensation.” ** (Steven Weinberg, “The Forces of Nature,” American Scientist, Vol. 65, March-April 1977, p.175.) Following this line of thinking, some researchers are tempted to visualize ultimate mathematical laws that apply to all the phenomena of the universe and that represent the underlying basis of reality. Many scientists regard the discovery of such laws as the final goal of their quest to understand nature.
Up until now, of course, no one has formulated a mathematically consistent universal theory of this kind, and the partial attempts that have been made involve a formidable tangle of unresolved technical difficulties. It is possible, however, for us to give a fairly complete description of the laws involved in our simple model universe, and by studying this model we can gain some insight into the feasibility of the physicists’ reaching their ultimate goal. As we shall see, their goal is actually unattainable, for it is vitiated by a serious fallacy in the interpretation of one of its underlying theoretical concepts-the concept of absolute chance.
Where Are the Details?
When we examine the laws of our model universe, we find that they adequately describe the deterministic functioning of the electrical apparatus and also the statistical properties’ of the sequence of radioactive decays. They do not, however, say anything about the details of this sequence. Indeed, according to our theory of the model universe, we cannot expect this sequence to display any systematic patterns that would enable us to describe it succinctly. We may therefore raise the following questions: Can our theoretical description of the model universe really be considered complete or universal? For the description to be complete, wouldn’t we need to incorporate into it a detailed description of the actual sequence of radioactive decays?
Considering these questions, we note that if we were to augment the theory in this way, then by no means could we consider the resulting enlarged theory unified. It would consist of a short list of basic laws followed by a very long list of data displaying no coherent pattern. Yet, if we did not include the exact sequence of radioactive decays, we would have to admit that our theory was incomplete in that it failed to account for this detailed information. Clearly, we could consider such a theory complete only if we adopted a standard of completeness that enabled us to ignore most of the detailed features of the very phenomena our theory was intended to describe.
Now, when we consider the concept of absolute chance, we see that it seems to provide just such a standard of completeness. The idea that a sequence of events is generated by causeless chance seems intuitively to imply that these events should be disorderly, chaotic, and meaningless. We would not expect one totally random sequence to be distinguishable in any significant way from any of the innumerable other random sequences having the same basic statistical properties. We would expect the details of the sequence to amount to nothing more than a display of pointless arbitrariness.
This leads naturally to the idea that one may consider a theoretical description of phenomena complete as long as it thoroughly accounts for the statistical properties of the phenomena. According to this idea, if the phenomena involve random sequences of events-in other words, sequences satisfying the statistical criteria for randomness—then these sequences must be products of causeless chance. As such, their detailed patterns must be meaningless and insignificant, and we can disregard them. Only the overall statistical features of the phenomena are worthy of theoretical description.
This method of defining the completeness of theories might seem satisfactory when applied to our example of radioactive decay. Certainly the observed patterns of atomic breakdown in radioactive substances seem completely chaotic. But let us look again at the sample history of our model universe depicted in figure 2. As we have already indicated, this history satisfies many of the criteria for a random sequence that can be deduced from our simple statistical laws. It also appears chaotic and disorderly. Yet if we examine it more closely, we find that it is actually a message expressed in binary code.
When we decipher this message it turns out, strangely enough, to consist of the following statement in English:
The probability of repetition of terrestrial evolution is zero. The same holds for the possibility that if most life on earth were destroyed, the evolution would start anew from some few primitive survivors. That evolution would be most unlikely to give rise to new manlike beings.
What are we to make of this? Could it be that by some extremely improbable accident, the random process corresponding to our simple statistical law just happened to generate this particular sequence? Using the law, we can calculate the probability of this, and we obtain a percentage of .000. . . (292 zeros) . . . 0001.
Data Compression
The answer, of course, is that we did not actually produce the sequence in figure 2 by a random process. That a sequence of events obeys a statistical law does not imply that a process of chance governed by this law actually produced the sequence. In fact, the sequence in figure 2 demonstrates that at least in some situations, the presence of a high degree of randomness in a sequence calls for a completely different interpretation. When we consider the method used to construct this sequence, we see that its apparent randomness results directly from the fact that it encodes a large amount of meaningful information.
We produced the sequence in figure 2 by a technique from the field of communications engineering known as “data compression.” In this field, engineers confront the problem of how to send as many messages as possible across a limited communications channel, such as a telephone line. They have therefore sought methods of encoding messages as sequences of symbols that are as short as possible but can still be readily decoded to reproduce the original message.
In 1948 Claude Shannon established some of the fundamental principles of data compression. ** (Claude E. Shannon, “A Mathematical Theory of Communication,” Bell System Technical Journal, Vol. 27, July 1948, p.379.) He showed that each message has a certain information content, which can be expressed as a number of “bits,” or binary ones and zeros. If a message contains n bits of information, we can encode it as a sequence of n or more ones and zeros, but we cannot encode it as a shorter sequence without losing part of the message. When we encode the message as a sequence of almost exactly n ones and zeros, its density of information is maximal, and each zero or one carries essential information.
Shannon showed that when encoded in the shortest possible sequence, a message appears to be completely random. The basic reason for this is that if patterns of ones and zeros are to be used in the most efficient possible way to encode information, all possible patterns must be used with roughly equal frequency. Thus the criteria for maximal information density and maximal randomness turn out to be the same.
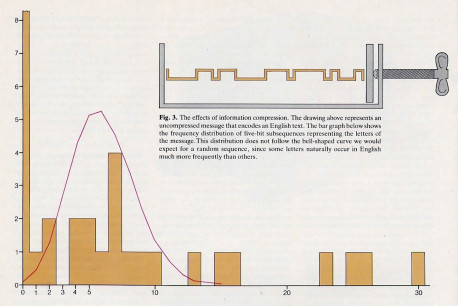
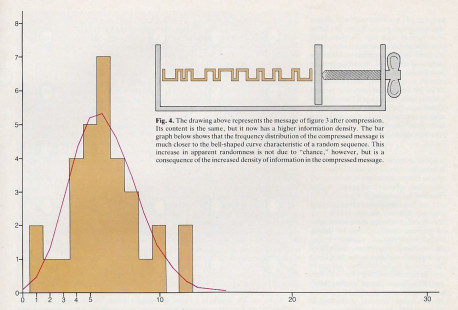
Figures 3 and 4 show the effects of information compression for the message encoded in figure 2. Figure 3 illustrates some of the characteristics of an uncompressed binary encoding of this message. The bar graph in this figure represents the frequency distribution for five-bit subsequences, each representing a letter of the English text. This distribution clearly does not follow the bell-shaped curve we would expect for a random sequence. However, when we encode the message in compressed form, as in figure 2, we obtain the distribution shown by the bar graph in figure 4. Here we see that simply by encoding the message in a more succinct form, we have greatly increased its apparent randomness. ** (This sequence was encoded using a method devised by (D. A. Huffman, “A Method for the Construction of Minimum Redundancy Codes,” Proceedings of the LR.E., Vol.40, Sept. 1952, p. 1098). As it stands, the sequence is highly random, but not fully so, since it still contains the redundancy caused by the repetition of words such as “evolution.” Thus further compression and consequent randomization are possible.)
We can conclude that it is not justifiable to insist upon absolute chance as an explanation of apparent randomness in nature. If a sequence of events exhibits the statistical properties of randomness, this may simply mean that it contains a large amount of significant information. Also, if a sequence exhibits a combination of random features and systematic features, as with our text before compression, this may reflect the presence of significant information in a less concentrated form. In either case, we would clearly be mistaken to disregard the details of the sequence, thinking them simply products of chance.
Implications for Evolution
At this point let us consider how these observations bear on the actual universe in which we live. Could it be that while focusing on ultimate mechanistic laws, modern scientists are disregarding some significant information encoded in the phenomena of nature? In fact, this is the implication of the sequence in figure 2 when we decode it and perceive its higher meaning-namely, as a statement about human evolution. The source of this statement is the prominent evolutionist Theodosius Dobzhansky, ** (Theodosius Dobzhansky, “From Potentiality to Realization in Evolution,” Mind in Nature, eds. J. B. Cobb Jr. & D. R. Griffin (Washington, D.C.: University Press of America, 1978), p.20.) who here expresses a view held widely among researchers in the life sciences. Dobzhansky is visualizing the origin of human life in the context of an underlying physical theory that involves combined processes of causation and chance. He is expressing the conviction that although such processes have generated the highly complex forms of human life we know, they nonetheless have a zero probability of doing so.
No one has shown, of course, that the universe as a whole, or even the small part of it we inhabit, really does obey some fundamental mechanistic laws. Yet suppose, for the sake of argument, that it does. In effect, Dobzhansky is asserting that from the viewpoint of this ultimate universal theory, the detailed information specifying the nature and history of human life is simply random noise. ** (We should note that in his article Dobzhansky does not clearly define his conception of the ultimate principles underlying the phenomena of the universe. He says that evolution is not acausal, that it is not due to pure chance, and that it is due to many interacting causal chains. Yet he also says that evolution is not rigidly predestined. He says that the course of evolution was not programmed or encoded into the primordial universe, but that primordial matter had the potential for giving rise to all forms of life, including innumerable unrealized forms. He speaks of evolution in terms of probabilities and stresses that the probability of the development of life as we know it is zero. It appears that Dobzhansky is thinking in terms of causal interactions that include, at some point, some mysterious element of absolute chance. We can conclude only that his thinking is muddled. We suggest that the reason for this is that although he needs the concept of absolute chance to formulate his evolutionary world view, at the same time he recognizes the illogical nature of this concept and would like to avoid it. Thus, he is caught in a dilemma.) The theory will be able to describe only broad statistical features of this information, and will have to dismiss its essential content as the vagaries of causeless chance.
The underlying basis for Dobzhansky’s conviction is that he and his fellow evolutionists have not been able to discern in nature any clearly definable pattern of cause and effect that enables them to deduce the forms of living organisms from basic physical principles. Of course, evolutionists customarily postulate that certain physical processes called mutation and natural selection have produced all living organisms. But their analysis of these processes has given them no insight into why one form is produced and not some other, and they have generally concluded that the appearance of specific forms like tigers, horses, and human beings is simply a matter of chance. This is the conclusion shown, for example, by Charles Darwin’s remark that “there seems to be no more design in the variability of organic beings, and in the action of natural selection, than in the course which the wind blows.” ** (Charles Darwin, The Life and Letters of Charles Darwin, ed. Frances Darwin, Vol.1 (New York: D. Appleton, 1896), p.20.)
Now, one might propose that in the future it will become possible to deduce the appearance of particular life forms from basic physical laws, But how much detail can we hope to obtain from such deductions? Will it be possible to deduce the complex features of human personality from fundamental physical laws? Will it be possible to deduce from such laws the detailed life histories of individual persons and to specify, for example, the writings of Theodosius Dobzhansky? Clearly there must be some limit to what we can expect from deductions based on a fixed set of relatively simple laws.
A Dilemma
These questions pose a considerable dilemma for those scientists who would like to formulate a complete and unified mechanistic theory of the universe, If we reject the unjustifiable concept of absolute chance, we see that a theory—if it is to be considered complete—must directly account for the unlimited diversity actually existing in reality. Either scientists must be satisfied with an incomplete theory that says nothing about the detailed features of many aspects of the universe-including life—or they must be willing to append to their theory a seemingly arbitrary list of data that describes these features at the cost of destroying the theory’s unity.
We can further understand this dilemma by briefly considering the physical theories studied before the advent of quantum mechanics and the formal introduction of absolute chance into science. Based solely on causal interactions, these theories employed the idea of chance only to describe an observer’s incomplete knowledge of the precisely determined flow of actual events, Although newer developments have superseded these theories, one might still wonder how effective they might be in providing a unified description of nature. We shall show by a simple example that these theories are confronted by the same dilemma that faces universal theories based on statistical laws.

Figure 5 depicts a rectangular array of evenly spaced spheres. Let us suppose that the positions of these spheres are fixed and that the array extends in all directions without limit. We shall consider the behavior of a single sphere that moves according to the laws of classical physics and rebounds elastically off the other spheres. We can imagine that once we set the single sphere into motion, it will continue to follow a zigzag path through the fixed array of spheres.
Figure 5 illustrates how a slight variation in the direction of the moving sphere can be greatly magnified when it bounces against one of the fixed spheres. On successive bounces this variation will increase more and more, and we would therefore have to know the sphere’s initial direction of motion with great accuracy to predict its path correctly for any length of time. For example, suppose the moving sphere is going sixty miles per hour, and the dimensions of the spheres are as shown in the figure. To predict the moving sphere’s path from bounce to bounce for one hour, we would have to know its original direction of motion (in degrees) with an accuracy of roughly two million decimal places. ** (We assume that the diameter of the spheres is 1/4 inch. If there is an average movement of about two inches between bounces, then a slight variation in direction will be magnified by an average of at least sixteen times per bounce. Consequently, an error in the nth decimal place in the direction of motion will begin to affect the first decimal place after about .83n bounces.) We can estimate that a number with this many decimal digits would take a full 714 pages to write down,
In effect, the number representing the initial direction of the sphere constitutes a script specifying in advance the detailed movements of the sphere for one hour. To specify the sphere’s movements for one year, this script would have to be expanded to more than six million pages. We can therefore see that this simple deterministic theory can provide complete predictions about the phenomena being studied-namely, the movements of the sphere—only if a detailed description of what will actually happen is first built into the theory.
We I can generalize the example of the bouncing sphere by allowing all the spheres to move simultaneously and to interact not merely by elastic collision but by force laws of various kinds. By doing this we obtain the classical Newtonian theory of nature mentioned by Hermann Helmholtz in the quotation cited at the beginning of this article. Helmholtz and many other scientists of his time wished to account for all phenomena by this theory, which was based entirely on simple laws of attraction and repulsion between material particles.
Encoding a Rhinoceros?
Let us therefore consider what this theory implies about the origin of life. Although it is more complicated than our simple example, this theory has some of the same characteristics. To account for life as we know it, the theory would have to incorporate billions of numbers describing the state of the world at some earlier time, and the entire history of living beings would have to be encoded in the high-order decimal digits of those numbers. Some of these decimal digits would encode the blueprints for a future rhinoceros, and others would encode the life history of a particular human being.
These digits would encode the facts of universal history in an extremely complicated way, and as far as the theory is concerned this encoded information would be completely arbitrary. This might tempt an adherent of the theory to abandon the idea of strict determinism and say—perhaps covertly—that the encoded information must have arisen by absolute chance (see note 6). Yet we have seen that this is a misleading idea, and it certainly has no p[ace in a theory based solely on causal interactions. All we can realistically say in the context of this theory is that the facts of universal history simply are what they are. The theory can describe them only if a detailed script is initially appended to it.
We can conclude that the prospects for a simple, universal mechanistic theory are not good. Once we eliminate the unsound and misleading idea of absolute chance, we are confronted with the problem of accounting for an almost unlimited amount of detailed information with a finite system of formulas. Some of this information may seem meaningless and chaotic, but a substantial part of it is involved with the phenomena of life, and this part includes the life histories of all scientific theorists. We must regard a theory that neglects most of this information as only a partial description of some features of the universe. Conversely, a theory that takes large amounts of this information into account must be filled with elaborate detail, and it can hardly be considered simple or unified.
An Alternative World View
It seems that on the platform of finite mathematical description, the ideal of unity is incompatible with the diversity of the real world. But this does not mean that the goal of finding unity and harmony in nature must be abandoned. In the remainder of this article we will introduce an alternative to the mechanistic view of the universe. This alternative, known as sanatana-dharma, is expounded in the Vedic literatures of India, such as Bhagavad-gita, Srimad-Bhagavatam, and Brahma-samhita. According to sanatana-dharma, while the variegated phenomena of the universe do indeed arise from a single, unified source, one can understand the nature of this source only by transcending the mechanistic world view.
Those who subscribe to a mechanistic theory of nature express all theoretical statements in terms of numbers, some of which they hope correspond to fundamental entities lying at the basis of observable phenomena. Mechanistic theorists therefore regard the fundamental constituents of reality as completely representable by numerical magnitudes. An example is the electron, which modern physics characterizes by numbers representing its mass, charge, and spin.
In Sanatana-dharma, however, conscious personality is accepted as the irreducible basis of reality. The ultimate source of all phenomena is understood to be a Supreme Personality, who possesses many personal names, such as Krsna and Govinda. This primordial person fully possesses consciousness, senses, knowledge, will, and all other personal features. According to sanatana-dharma, all of these attributes are absolute, and it is not possible to reduce them to the mathematically describable interaction of some simple entities corresponding to sets of numbers. Rather, all the variegated phenomena of the universe, including the phenomena of life, are manifestations of the energy of the Supreme Person, and one can fully understand them only in relation to this original source.
The unity of the Absolute Person is a basic postulate of sanatana-dharma. Krsna is unique and indivisible, yet He simultaneously possesses unlimited personal opulences, and He is the original wellspring of all the diverse phenomena of the universe. This idea may seem contradictory, but we can partially understand it if we consider that, according to sanatana-dharma, conscious personality has the attributes of infinity.
A few simple examples will serve to illustrate the properties of infinity. Consider a finite set of, say, one hundred points. We can regard this set as essentially disunited, since any part of it has fewer points than the whole and is therefore different from the whole. In this sense, the only unified set is the set consisting of exactly one point. In contrast to this, consider a continuous line one unit long. If we select any small segment of this line, no matter how short, we can obtain the entire line by expanding this segment. Thus the line has unity in the sense that it is equivalent to its parts. This is so because the line has infinitely many parts.
Although the above example is crude, it will serve as a metaphor to illustrate the difference between the Supreme Person and the hypothetical physical processes in mechanistic theories. A mechanistic theory based on a finite system of mathematical expressions can be truly unified only if it can be reduced to one symbol-a single binary digit of 0 or 1. Correspondingly, an underlying physical process characterized theoretically by a finite set of attributes can be unified only if it is devoid of all properties. Of course, a theory that described the world in this way would say nothing at all, and mechanistic theorists have had to settle for the goal of seeking the simplest possible theory that can adequately describe nature. Unfortunately, we have seen that the simplest adequate theory must be almost unlimitedly complex.
In contrast to mechanistic theories, sanatana-dharma teaches that while the Supreme Person possesses unlimited complexity, He is simultaneously nondifferent from His parts and is therefore a perfect unit. The Brahma-samhita (5.32) expresses this idea; “Each of the limbs of Govinda, the primeval Lord, possesses the full-fledged functions of all the organs. and each limb eternally manifests, sees, and maintains the infinite universes, both spiritual and mundane.” Even though Krsna has distinct parts, each part is the total being of Krsna. This characteristic of the Supreme Person is dimly reflected in our example of the line, but there is a significant difference. The equivalence of the line to its parts depends on an externally supplied operation of expansion, and thus the unity of the line exists only in the mind of an observer (as does the line itself, for it is only an abstraction). In contrast, the identity of Krsna with His parts is inherent in the reality of Krsna Himself, and His unity is therefore complete and perfect.
The Supreme and His Energies
According to sanatana-dharma, the material universe we live in is the product of two basic energies of the Supreme Person. One of these, the external energy, comprises what are commonly known as matter and energy. The patterns and transformations of the external energy produce all the observable phenomena of the universe. Thus, the measurable aspects of this energy constitute the subject matter of modern, mechanistic science.
Sanatana-dharma teaches that the activity of the external energy is completely determined by the will of Krsna. At first glance, this might seem incompatible with our knowledge of physics, for it would seem that some phenomena of nature do follow rigid, deterministic laws that we can describe by simple mathematical formulas. But there is no real contradiction here. Just as a human being can draw circles and other curves obeying simple mathematical laws, so the Supreme Person can easily impose certain mathematical regularities on the behavior of matter in the universe as a whole.
We can better understand the relationship between Krsna and the phenomenal universe if we again consider the concept of infinity. The Vedic literature states that Krsna is fully present within all the atoms of the universe and that He is at the same time an undivided, independent being completely distinct from the universe. Krsna directly superintends all the phenomena of the universe in complete detail; but since He is unlimited, these details occupy only an infinitesimal fraction of His attention, and He can there-fore simultaneously remain completely aloof from the universal manifestation.
Here one might object that if all the phenomena of the universe follow the will of a supremely intelligent being, why do so many of these phenomena appear chaotic and meaningless?
Part of the answer to this question is that meaningful patterns may appear random if they contain a high density of information. We have seen that such complex patterns tend to obey certain statistical laws simply as a result of their large information content. Thus a complex, seemingly random pattern in nature may actually be meaningful, even though we do not understand it.
Another part of the answer is that meaningful patterns can easily change into meaningless patterns. Consider how a number of meaningful conversations, when heard simultaneously in a crowded room, merge into a meaningless din. Such meaningless patterns will inherit the statistical properties of their meaningful sources and will appear as undecipherable “random noise.”
These considerations enable us to understand how apparent meaninglessness and chaos can arise in nature, but they tell us nothing about the ultimate definition of meaning itself. In general, mechanistic theorists have not been able to give a satisfactory definition of meaning or purpose within the framework of the mechanistic world view. But sanatana-dharma does provide such a definition, and this involves the second of the two basic energies of Krsna that make up the material universe.
The second energy, known as the internal energy of Krsna, includes the innumerable sentient entities, called atmas. Sanatana-dharma teaches that each living organism consists of an atma in association with a physical body composed of external energy. The atma is the actual conscious self of the living organism, whereas the physical body is merely an insentient vehicle or machine. Each atma is an irreducible conscious personality, possessing senses, mind, intelligence, and all other personal faculties. These individual personalities are minute fragmental parts of the Supreme Person, and as such they possess His qualities in minute degree.
In the embodied state the atma’s natural senses are linked with the sensory apparatus of the body, and so the atma receives all its information about the world through the bodily senses. Likewise, the embodied atma’s will can act only through various bodily organs. This interaction between the atma and the material apparatus of the body does not involve a direct link. Rather, this interaction is mediated by the Supreme Person, who manipulates the external energy in a highly complex fashion according to both the desires of the atmas and His own higher plan.
The embodied condition is not natural for the atma. The atma is one in quality with Krsna, and thus he is eternally connected with Him through a constitutional relationship of loving reciprocation. This relationship of direct personal exchange involves the full use of all the atma’s personal faculties, and as such it defines the ultimate meaning and purpose of individual conscious personality. Yet in the embodied state the atma is largely unaware of this relationship. The purpose of Krsna’s higher plan, then, is to reawaken the embodied atmas and gradually restore them to their natural state of existence.
Conclusion
It is this higher plan that determines the ultimate criterion of meaningfulness for the phenomena of the universe. Under the direction of the single Supreme Person, the external energy undergoes highly complex transformations that are related to the desires and activities of the innumerable conscious entities. These transformations involve the continuous imposition of intricate patterns on the distribution of matter, the combination and recombination of these patterns according to various systematic laws, and the gradual degradation of these patterns into a welter of cosmic “random noise.” Seen from a purely mechanistic perspective, the measurable behavior of the external energy seems a complex but arbitrary combination of regularity and irregularity. But in the midst of this bewildering display of phenomena, the Supreme Person is continuously making arrangements for the atmas to realize their true nature.
In the ultimate issue, this activity by the Supreme Person is the key to understanding the entire cosmic manifestation. The process whereby the atma can achieve enlightenment is the principal subject matter of sanatana-dharma. And, in fact, sanatana-dharma is itself part of that process. This subject involves many detailed considerations, and here we have only introduced a few basic points that relate to the topics of chance and universal unity. In conclusion, we will simply note that by pursuing the process of self-realization described in sanatana-dharma, a person can acquire direct understanding of the unified source underlying the phenomena of the universe.
Readers interested in the subject matter of this article are invited to correspond with the author at 72 Commonwealth Avenue, Boston, Massachusetts 02116.
SADAPUTA DASA studied at the State University of New York and Syracuse University and later received a National Science Fellowship. He went on to complete his Ph.D. in mathematics at Cornell, specializing in probability theory and statistical mechanics.

Leave a Reply